Das Modul gehört zu den Dingen, von denen scheinbar jeder gehört hat, die aber in Wirklichkeit niemand wirklich versteht. Daher wird es heute eine große Lektion geben, die dem Lösen von Gleichungen mit Modulen gewidmet ist.

Ich sage gleich: Die Lektion wird nicht schwer sein. Und generell sind Module ein relativ einfaches Thema. „Ja natürlich, es ist nicht kompliziert! Es haut mich um!“ - werden viele Studenten sagen, aber all diese Gehirnbrüche entstehen dadurch, dass die meisten Menschen kein Wissen im Kopf haben, sondern irgendeinen Mist. Und das Ziel dieser Lektion ist es, Mist in Wissen zu verwandeln. :)

Eine kleine Theorie

So lass uns gehen. Beginnen wir mit dem Wichtigsten: Was ist ein Modul? Ich möchte Sie daran erinnern, dass der Modul einer Zahl einfach dieselbe Zahl ist, jedoch ohne das Minuszeichen. Das ist zum Beispiel $\left| -5 \right|=5$. Oder $\left| -129,5 \right|=$129,5.

Ist das so einfach? Ja, einfach. Was ist dann der absolute Wert einer positiven Zahl? Hier ist es noch einfacher: Der Modul einer positiven Zahl ist gleich dieser Zahl selbst: $\left| 5 \right|=5$; $\left| 129,5 \right|=$129,5 usw.

Es stellt sich als merkwürdig heraus: Verschiedene Zahlen können das gleiche Modul haben. Beispiel: $\left| -5 \right|=\left| 5 \right|=5$; $\left| -129,5 \right|=\left| 129,5\richtig|=$129,5. Es ist leicht zu erkennen, was das für Zahlen sind, deren Module gleich sind: Diese Zahlen sind entgegengesetzt. Daher stellen wir selbst fest, dass die Module entgegengesetzter Zahlen gleich sind:

\[\left| -a \right|=\left| a\richtig|\]

Noch ein wichtiger Fakt: Modul ist niemals negativ. Welche Zahl wir auch immer nehmen – sei sie positiv oder negativ – ihr Modul ist immer positiv (oder im Extremfall Null). Aus diesem Grund wird der Modul oft als Absolutwert einer Zahl bezeichnet.

Wenn wir außerdem die Definition des Moduls für eine positive und eine negative Zahl kombinieren, erhalten wir eine globale Definition des Moduls für alle Zahlen. Nämlich: Der Modul einer Zahl ist gleich der Zahl selbst, wenn die Zahl positiv (oder Null) ist, oder gleich der entgegengesetzten Zahl, wenn die Zahl negativ ist. Sie können dies als Formel schreiben:

Es gibt auch einen Modul von Null, der jedoch immer gleich Null ist. Außerdem ist Null die einzige Zahl, die kein Gegenteil hat.

Betrachten wir also die Funktion $y=\left| x \right|$ und versuchen Sie, seinen Graphen zu zeichnen. Sie erhalten etwa Folgendes:

Moduldiagramm und Beispiel zur Lösung der Gleichung

Aus diesem Bild ist sofort klar, dass $\left| -m \right|=\left| m \right|$, und der Modulgraph fällt nie unter die x-Achse. Aber das ist noch nicht alles: Die rote Linie markiert die Gerade $y=a$, die uns für positives $a$ zwei Wurzeln gleichzeitig liefert: $((x)_(1))$ und $((x) _(2)) $, aber darüber reden wir später. :)

Neben der rein algebraischen Definition gibt es eine geometrische. Nehmen wir an, es gibt zwei Punkte auf der Zahlengeraden: $((x)_(1))$ und $((x)_(2))$. In diesem Fall ist der Ausdruck $\left| ((x)_(1))-((x)_(2)) \right|$ ist einfach der Abstand zwischen den angegebenen Punkten. Oder, wenn Sie es vorziehen, die Länge des Segments, das diese Punkte verbindet:

Der Modul ist der Abstand zwischen Punkten auf einer Zahlengeraden

Diese Definition impliziert auch, dass der Modul immer nicht negativ ist. Aber genug Definitionen und Theorie – kommen wir zu echten Gleichungen. :)

Grundformel

Okay, wir haben die Definition geklärt. Aber das hat es nicht einfacher gemacht. Wie löst man Gleichungen, die genau dieses Modul enthalten?

Ruhig, einfach ruhig. Beginnen wir mit den einfachsten Dingen. Betrachten Sie etwa Folgendes:

\[\left| x\right|=3\]

Der Modul von $x$ ist also 3. Was könnte $x$ sein? Nun, der Definition nach zu urteilen, sind wir mit $x=3$ recht zufrieden. Wirklich:

\[\left| 3\right|=3\]

Gibt es noch andere Zahlen? Cap scheint anzudeuten, dass dies der Fall ist. Beispielsweise ist $x=-3$ auch $\left| -3 \right|=3$, d.h. die geforderte Gleichheit ist erfüllt.

Wenn wir also suchen und nachdenken, finden wir vielleicht mehr Zahlen? Aber seien wir ehrlich: Es gibt keine Zahlen mehr. Gleichung $\left| x \right|=3$ hat nur zwei Wurzeln: $x=3$ und $x=-3$.

Jetzt machen wir die Aufgabe etwas komplizierter. Lassen Sie die Funktion $f\left(x \right)$ unter dem Modulzeichen anstelle der Variablen $x$ hängen und setzen Sie eine beliebige Zahl $a$ anstelle des Tripels auf der rechten Seite. Wir erhalten die Gleichung:

\[\left| f\left(x \right) \right|=a\]

Wie können wir das also lösen? Ich möchte Sie daran erinnern: $f\left(x \right)$ ist eine beliebige Funktion, $a$ ist eine beliebige Zahl. Diese. Überhaupt alles! Zum Beispiel:

\[\left| 2x+1 \right|=5\]

\[\left| 10x-5 \right|=-65\]

Achten wir auf die zweite Gleichung. Über ihn kann man sofort sagen: Er hat keine Wurzeln. Warum? Alles ist richtig: Weil es erfordert, dass der Modul gleich einer negativen Zahl ist, was nie passiert, da wir bereits wissen, dass der Modul immer eine positive Zahl oder im Extremfall Null ist.

Aber mit der ersten Gleichung macht alles mehr Spaß. Es gibt zwei Möglichkeiten: Entweder gibt es einen positiven Ausdruck unter dem Modulzeichen und dann $\left| 2x+1 \right|=2x+1$, oder dieser Ausdruck ist immer noch negativ, und dann $\left| 2x+1 \right|=-\left(2x+1 \right)=-2x-1$. Im ersten Fall wird unsere Gleichung wie folgt umgeschrieben:

\[\left| 2x+1 \right|=5\Rightarrow 2x+1=5\]

Und plötzlich stellt sich heraus, dass der submodulare Ausdruck $2x+1$ wirklich positiv ist – er ist gleich der Zahl 5. Das heißt Wir können diese Gleichung sicher lösen – die resultierende Wurzel wird ein Teil der Antwort sein:

Wer besonders misstrauisch ist, kann versuchen, die gefundene Wurzel in die ursprüngliche Gleichung einzusetzen und sicherzustellen, dass unter dem Modul tatsächlich eine positive Zahl steht.

Schauen wir uns nun den Fall eines negativen submodularen Ausdrucks an:

\[\left\( \begin(align)& \left| 2x+1 \right|=5 \\& 2x+1 \lt 0 \\\end(align) \right.\Rightarrow -2x-1=5 \Rightarrow 2x+1=-5\]

Hoppla! Auch hier ist alles klar: Wir haben angenommen, dass $2x+1 \lt 0$ ist, und als Ergebnis haben wir erhalten, dass $2x+1=-5$ – tatsächlich ist dieser Ausdruck kleiner als Null. Wir lösen die resultierende Gleichung und wissen bereits sicher, dass die gefundene Wurzel zu uns passt:

Insgesamt haben wir wieder zwei Antworten erhalten: $x=2$ und $x=3$. Ja, der Rechenaufwand fiel etwas größer aus als bei der sehr einfachen Gleichung $\left| x \right|=3$, aber grundsätzlich hat sich nichts geändert. Vielleicht gibt es also eine Art universellen Algorithmus?

Ja, einen solchen Algorithmus gibt es. Und jetzt werden wir es analysieren.

Das Modulzeichen loswerden

Gegeben sei uns die Gleichung $\left| f\left(x \right) \right|=a$ und $a\ge 0$ (ansonsten gibt es, wie wir bereits wissen, keine Wurzeln). Dann können Sie das Modulzeichen mithilfe der folgenden Regel entfernen:

\[\left| f\left(x \right) \right|=a\Rightarrow f\left(x \right)=\pm a\]

Somit teilt sich unsere Gleichung mit einem Modul in zwei Teile, jedoch ohne Modul. Das ist alles, was die Technologie ausmacht! Versuchen wir, ein paar Gleichungen zu lösen. Beginnen wir damit

\[\left| 5x+4 \right|=10\Rightarrow 5x+4=\pm 10\]

Betrachten wir getrennt, wann rechts eine Zehn plus steht, und getrennt, wann rechts ein Minus steht. Wir haben:

\[\begin(align)& 5x+4=10\Rightarrow 5x=6\Rightarrow x=\frac(6)(5)=1,2; \\& 5x+4=-10\Rightarrow 5x=-14\Rightarrow x=-\frac(14)(5)=-2.8. \\\end(align)\]

Das ist alles! Wir haben zwei Wurzeln: $x=1,2$ und $x=-2,8$. Die gesamte Lösung umfasste buchstäblich zwei Zeilen.

Ok, keine Frage, schauen wir uns etwas Ernsthafteres an:

\[\left| 7-5x\right|=13\]

Wieder öffnen wir das Modul mit Plus und Minus:

\[\begin(align)& 7-5x=13\Rightarrow -5x=6\Rightarrow x=-\frac(6)(5)=-1,2; \\& 7-5x=-13\Rightarrow -5x=-20\Rightarrow x=4. \\\end(align)\]

Noch ein paar Zeilen – und die Antwort ist fertig! Wie gesagt, Module sind nichts Kompliziertes. Sie müssen sich nur ein paar Regeln merken. Deshalb gehen wir weiter und beginnen mit wirklich komplexeren Aufgaben.

Der Fall einer rechten Variablen

Betrachten Sie nun diese Gleichung:

\[\left| 3x-2 \right|=2x\]

Diese Gleichung unterscheidet sich grundlegend von allen vorherigen. Wie? Und die Tatsache, dass rechts vom Gleichheitszeichen der Ausdruck $2x$ steht – und wir nicht im Voraus wissen können, ob er positiv oder negativ ist.

Was ist in diesem Fall zu tun? Zuerst müssen wir das ein für alle Mal verstehen Wenn sich herausstellt, dass die rechte Seite der Gleichung negativ ist, hat die Gleichung keine Wurzeln- Wir wissen bereits, dass der Modul nicht gleich einer negativen Zahl sein kann.

Und zweitens, wenn der rechte Teil noch positiv (oder gleich Null) ist, dann können Sie genauso vorgehen wie zuvor: Öffnen Sie das Modul einfach separat mit einem Pluszeichen und separat mit einem Minuszeichen.

Daher formulieren wir eine Regel für beliebige Funktionen $f\left(x \right)$ und $g\left(x \right)$ :

\[\left| f\left(x \right) \right|=g\left(x \right)\Rightarrow \left\( \begin(align)& f\left(x \right)=\pm g\left(x \right ), \\& g\left(x \right)\ge 0. \\\end(align) \right.\]

Bezogen auf unsere Gleichung erhalten wir:

\[\left| 3x-2 \right|=2x\Rightarrow \left\( \begin(align)& 3x-2=\pm 2x, \\& 2x\ge 0. \\\end(align) \right.\]

Nun ja, mit der Anforderung $2x\ge 0$ werden wir irgendwie zurechtkommen. Am Ende können wir dummerweise die Wurzeln ersetzen, die wir aus der ersten Gleichung erhalten, und prüfen, ob die Ungleichung gilt oder nicht.

Lösen wir also die Gleichung selbst:

\[\begin(align)& 3x-2=2\Rightarrow 3x=4\Rightarrow x=\frac(4)(3); \\& 3x-2=-2\Rightarrow 3x=0\Rightarrow x=0. \\\end(align)\]

Nun, welche dieser beiden Wurzeln erfüllt die Anforderung $2x\ge 0$? Ja beides! Daher wird die Antwort zwei Zahlen sein: $x=(4)/(3)\;$ und $x=0$. Das ist die Lösung. :)

Ich vermute, dass sich einige der Schüler bereits langweilen? Schauen wir uns eine noch komplexere Gleichung an:

\[\left| ((x)^(3))-3((x)^(2))+x \right|=x-((x)^(3))\]

Obwohl es böse aussieht, handelt es sich in Wirklichkeit immer noch um die gleiche Gleichung der Form „Modul gleich Funktion“:

\[\left| f\left(x \right) \right|=g\left(x \right)\]

Und es wird genauso gelöst:

\[\left| ((x)^(3))-3((x)^(2))+x \right|=x-((x)^(3))\Rightarrow \left\( \begin(align)& ( (x)^(3))-3((x)^(2))+x=\pm \left(x-((x)^(3)) \right), \\& x-((x )^(3))\ge 0. \\\end(align) \right.\]

Wir werden uns später mit der Ungleichheit befassen – sie ist irgendwie zu böse (eigentlich ist sie einfach, aber wir werden sie nicht lösen). Im Moment ist es besser, sich mit den resultierenden Gleichungen zu befassen. Betrachten wir den ersten Fall – dann wird das Modul mit einem Pluszeichen erweitert:

\[((x)^(3))-3((x)^(2))+x=x-((x)^(3))\]

Nun, es ist ein Kinderspiel, dass Sie alles von links sammeln, ähnliches mitbringen und sehen müssen, was passiert. Und das passiert:

\[\begin(align)& ((x)^(3))-3((x)^(2))+x=x-((x)^(3)); \\& 2((x)^(3))-3((x)^(2))=0; \\\end(align)\]

Wir nehmen den gemeinsamen Faktor $((x)^(2))$ aus der Klammer und erhalten eine sehr einfache Gleichung:

\[((x)^(2))\left(2x-3 \right)=0\Rightarrow \left[ \begin(align)& ((x)^(2))=0 \\& 2x-3 =0 \\\end(align) \right.\]

\[((x)_(1))=0;\quad ((x)_(2))=\frac(3)(2)=1,5.\]

Hier haben wir uns eine wichtige Eigenschaft des Produkts zunutze gemacht, um das ursprüngliche Polynom zu faktorisieren: Das Produkt ist gleich Null, wenn mindestens einer der Faktoren gleich Null ist.

Gehen wir nun genauso mit der zweiten Gleichung um, die man erhält, indem man den Modul um ein Minuszeichen erweitert:

\[\begin(align)& ((x)^(3))-3((x)^(2))+x=-\left(x-((x)^(3)) \right); \\& ((x)^(3))-3((x)^(2))+x=-x+((x)^(3)); \\& -3((x)^(2))+2x=0; \\& x\left(-3x+2 \right)=0. \\\end(align)\]

Wieder das Gleiche: Das Produkt ist gleich Null, wenn mindestens einer der Faktoren gleich Null ist. Wir haben:

\[\left[ \begin(align)& x=0 \\& -3x+2=0 \\\end(align) \right.\]

Nun, wir haben drei Wurzeln: $x=0$, $x=1,5$ und $x=(2)/(3)\;$. Nun, welche dieser Fragen werden in die endgültige Antwort einfließen? Denken Sie dazu daran, dass wir eine zusätzliche Einschränkung in Form einer Ungleichung haben:

Wie kann dieser Anforderung Rechnung getragen werden? Ersetzen wir einfach die gefundenen Wurzeln und prüfen, ob die Ungleichung für diese $x$ gilt oder nicht. Wir haben:

\[\begin(align)& x=0\Rightarrow x-((x)^(3))=0-0=0\ge 0; \\& x=1.5\Rightarrow x-((x)^(3))=1.5-((1.5)^(3)) \lt 0; \\& x=\frac(2)(3)\Rightarrow x-((x)^(3))=\frac(2)(3)-\frac(8)(27)=\frac(10) (27)\ge 0; \\\end(align)\]

Daher passt die Wurzel $x=1,5$ nicht zu uns. Und als Antwort wird es nur zwei Wurzeln geben:

\[((x)_(1))=0;\quad ((x)_(2))=\frac(2)(3).\]

Wie Sie sehen, gab es auch in diesem Fall nichts Kompliziertes – Gleichungen mit Modulen werden immer mit einem Algorithmus gelöst. Sie müssen lediglich ein gutes Verständnis für Polynome und Ungleichungen haben. Daher gehen wir zu komplexeren Aufgaben über – es wird bereits nicht ein, sondern zwei Module geben.

Gleichungen mit zwei Modulen

Bisher haben wir nur die einfachsten Gleichungen untersucht – es gab ein Modul und etwas anderes. Wir haben dieses „etwas anderes“ an einen anderen Teil der Ungleichung geschickt, weg vom Modul, sodass am Ende alles auf eine Gleichung der Form $\left| reduziert würde f\left(x \right) \right|=g\left(x \right)$ oder noch einfacher $\left| f\left(x \right) \right|=a$.

Aber der Kindergarten ist vorbei – es ist Zeit, über etwas Ernsthafteres nachzudenken. Beginnen wir mit Gleichungen wie dieser:

\[\left| f\left(x \right) \right|=\left| g\left(x \right) \right|\]

Dies ist eine Gleichung der Form „Modul ist gleich Modul“. Der grundsätzlich wichtige Punkt ist das Fehlen anderer Begriffe und Faktoren: nur ein Modul links, ein weiteres Modul rechts – und nichts weiter.

Jemand wird jetzt denken, dass solche Gleichungen schwieriger zu lösen sind als das, was wir bisher untersucht haben. Aber nein: Diese Gleichungen sind noch einfacher zu lösen. Hier ist die Formel:

\[\left| f\left(x \right) \right|=\left| g\left(x \right) \right|\Rightarrow f\left(x \right)=\pm g\left(x \right)\]

Alle! Wir setzen submodulare Ausdrücke einfach gleich, indem wir einem von ihnen ein Plus- oder Minuszeichen voranstellen. Und dann lösen wir die resultierenden beiden Gleichungen – und fertig sind die Wurzeln! Keine zusätzlichen Einschränkungen, keine Ungleichheiten usw. Alles ist sehr einfach.

Versuchen wir, dieses Problem zu lösen:

\[\left| 2x+3 \right|=\left| 2x-7 \right|\]

Elementarer Watson! Erweiterung der Module:

\[\left| 2x+3 \right|=\left| 2x-7 \right|\Rightarrow 2x+3=\pm \left(2x-7 \right)\]

Betrachten wir jeden Fall einzeln:

\[\begin(align)& 2x+3=2x-7\Rightarrow 3=-7\Rightarrow \emptyset ; \\& 2x+3=-\left(2x-7 \right)\Rightarrow 2x+3=-2x+7. \\\end(align)\]

Die erste Gleichung hat keine Wurzeln. Denn wann ist $3=-7$? Bei welchen Werten von $x$? „Was zum Teufel ist $x$? Bist du bekifft? Da gibt es überhaupt kein $x$“, sagen Sie. Und du wirst Recht haben. Wir haben eine Gleichheit erhalten, die nicht von der Variablen $x$ abhängt, und gleichzeitig ist die Gleichheit selbst falsch. Deshalb gibt es keine Wurzeln. :)

Mit der zweiten Gleichung ist alles etwas interessanter, aber auch sehr, sehr einfach:

Wie Sie sehen, wurde alles buchstäblich in ein paar Zeilen gelöst – wir haben von einer linearen Gleichung nichts anderes erwartet. :)

Als Ergebnis lautet die endgültige Antwort: $x=1$.

Und wie? Schwierig? Natürlich nicht. Versuchen wir etwas anderes:

\[\left| x-1 \right|=\left| ((x)^(2))-3x+2 \right|\]

Wieder haben wir eine Gleichung der Form $\left| f\left(x \right) \right|=\left| g\left(x \right) \right|$. Deshalb schreiben wir es sofort um und offenbaren das Modulzeichen:

\[((x)^(2))-3x+2=\pm \left(x-1 \right)\]

Vielleicht wird jetzt jemand fragen: „Hey, was für ein Unsinn?“ Warum erscheint „Plus-Minus“ auf der rechten Seite und nicht auf der linken Seite?“ Beruhige dich, ich erkläre dir jetzt alles. Tatsächlich hätten wir unsere Gleichung auf eine gute Art und Weise wie folgt umschreiben sollen:

Dann müssen Sie die Klammern öffnen, alle Terme auf eine Seite des Gleichheitszeichens verschieben (da die Gleichung in beiden Fällen natürlich quadratisch ist) und dann die Wurzeln finden. Aber Sie müssen zugeben: Wenn „Plus-Minus“ vor drei Begriffen steht (besonders wenn einer dieser Begriffe ein quadratischer Ausdruck ist), sieht es irgendwie komplizierter aus als die Situation, wenn „Plus-Minus“ vor nur zwei Begriffen steht.

Aber nichts hindert uns daran, die ursprüngliche Gleichung wie folgt umzuschreiben:

\[\left| x-1 \right|=\left| ((x)^(2))-3x+2 \right|\Rightarrow \left| ((x)^(2))-3x+2 \right|=\left| x-1 \right|\]

Was ist passiert? Nichts Besonderes: Sie haben nur die linke und rechte Seite vertauscht. Eine kleine Sache, die uns letztendlich das Leben ein wenig einfacher machen wird. :)

Im Allgemeinen lösen wir diese Gleichung, indem wir Optionen mit einem Plus und einem Minus berücksichtigen:

\[\begin(align)& ((x)^(2))-3x+2=x-1\Rightarrow ((x)^(2))-4x+3=0; \\& ((x)^(2))-3x+2=-\left(x-1 \right)\Rightarrow ((x)^(2))-2x+1=0. \\\end(align)\]

Die erste Gleichung hat Wurzeln $x=3$ und $x=1$. Das zweite ist im Allgemeinen ein exaktes Quadrat:

\[((x)^(2))-2x+1=((\left(x-1 \right))^(2))\]

Daher hat es nur eine Wurzel: $x=1$. Aber wir haben diese Wurzel bereits früher erhalten. Somit fließen nur zwei Zahlen in die endgültige Antwort ein:

\[((x)_(1))=3;\quad ((x)_(2))=1.\]

Mission erfüllt! Sie können einen Kuchen aus dem Regal nehmen und ihn essen. Es gibt 2 davon, deines ist das mittlere. :)

Wichtiger Hinweis. Das Vorhandensein identischer Wurzeln für verschiedene Varianten der Modulentwicklung bedeutet, dass die ursprünglichen Polynome faktorisiert werden und es unter diesen Faktoren definitiv eine gemeinsame geben wird. Wirklich:

\[\begin(align)& \left| x-1 \right|=\left| ((x)^(2))-3x+2 \right|; \\& \left| x-1 \right|=\left| \left(x-1 \right)\left(x-2 \right) \right|. \\\end(align)\]

Eine der Moduleigenschaften: $\left| a\cdot b \right|=\left| a \right|\cdot \left| b \right|$ (d. h. der Modul des Produkts ist gleich dem Produkt der Module), sodass die ursprüngliche Gleichung wie folgt umgeschrieben werden kann:

\[\left| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \right|\]

Wie Sie sehen, haben wir tatsächlich eine Gemeinsamkeit. Wenn Sie nun alle Module auf einer Seite sammeln, können Sie diesen Faktor aus der Halterung nehmen:

\[\begin(align)& \left| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \right|; \\& \left| x-1 \right|-\left| x-1 \right|\cdot \left| x-2 \right|=0; \\& \left| x-1 \right|\cdot \left(1-\left| x-2 \right| \right)=0. \\\end(align)\]

Denken Sie nun daran, dass das Produkt gleich Null ist, wenn mindestens einer der Faktoren gleich Null ist:

\[\left[ \begin(align)& \left| x-1 \right|=0, \\& \left| x-2 \right|=1. \\\end(align) \right.\]

Somit wurde die ursprüngliche Gleichung mit zwei Modulen auf die beiden einfachsten Gleichungen reduziert, über die wir gleich zu Beginn der Lektion gesprochen haben. Solche Gleichungen können buchstäblich in ein paar Zeilen gelöst werden. :)

Diese Bemerkung mag unnötig komplex und in der Praxis nicht anwendbar erscheinen. In Wirklichkeit können Sie jedoch auf viel komplexere Probleme stoßen als die, mit denen wir uns heute befassen. In ihnen können Module mit Polynomen, arithmetischen Wurzeln, Logarithmen usw. kombiniert werden. Und in solchen Situationen kann die Möglichkeit, den Gesamtgrad der Gleichung zu verringern, indem man etwas aus Klammern herausnimmt, sehr, sehr nützlich sein. :)

Nun möchte ich mir eine andere Gleichung ansehen, die auf den ersten Blick vielleicht verrückt erscheint. Viele Studierende bleiben dabei hängen, selbst diejenigen, die glauben, die Module gut zu verstehen.

Diese Gleichung ist jedoch noch einfacher zu lösen als die, die wir zuvor betrachtet haben. Und wenn Sie verstehen, warum, erhalten Sie einen weiteren Trick zum schnellen Lösen von Gleichungen mit Modulen.

Die Gleichung lautet also:

\[\left| x-((x)^(3)) \right|+\left| ((x)^(2))+x-2 \right|=0\]

Nein, das ist kein Tippfehler: Es ist ein Plus zwischen den Modulen. Und wir müssen herausfinden, bei welchem ​​$x$ die Summe zweier Module gleich Null ist. :)

Was ist überhaupt das Problem? Das Problem besteht jedoch darin, dass jedes Modul eine positive Zahl oder im Extremfall Null ist. Was passiert, wenn Sie zwei positive Zahlen addieren? Offensichtlich wieder eine positive Zahl:

\[\begin(align)& 5+7=12 \gt 0; \\& 0,004+0,0001=0,0041 \gt 0; \\& 5+0=5 \gt 0. \\\end(align)\]

Die letzte Zeile könnte Ihnen eine Idee geben: Die Summe der Module ist nur dann Null, wenn jedes Modul Null ist:

\[\left| x-((x)^(3)) \right|+\left| ((x)^(2))+x-2 \right|=0\Rightarrow \left\( \begin(align)& \left| x-((x)^(3)) \right|=0, \\& \left| ((x)^(2))+x-2 \right|=0. \\\end(align) \right.\]

Und wann ist der Modul gleich Null? Nur in einem Fall – wenn der submodulare Ausdruck gleich Null ist:

\[((x)^(2))+x-2=0\Rightarrow \left(x+2 \right)\left(x-1 \right)=0\Rightarrow \left[ \begin(align)& x=-2 \\& x=1 \\\end(align) \right.\]

Somit haben wir drei Punkte, an denen das erste Modul auf Null zurückgesetzt wird: 0, 1 und −1; sowie zwei Punkte, an denen das zweite Modul auf Null zurückgesetzt wird: −2 und 1. Da wir jedoch beide Module gleichzeitig auf Null zurücksetzen müssen, müssen wir unter den gefundenen Zahlen diejenigen auswählen, die in enthalten sind beide Sets. Offensichtlich gibt es nur eine solche Zahl: $x=1$ – das wird die endgültige Antwort sein.

Spaltungsmethode

Nun, wir haben bereits eine Reihe von Problemen behandelt und viele Techniken gelernt. Glaubst du, das ist alles? Aber nein! Nun schauen wir uns die finale Technik an – und gleichzeitig die wichtigste. Wir werden über die Aufteilung von Gleichungen mit dem Modul sprechen. Worüber werden wir überhaupt reden? Gehen wir etwas zurück und schauen wir uns eine einfache Gleichung an. Zum Beispiel dies:

\[\left| 3x-5 \right|=5-3x\]

Im Prinzip wissen wir bereits, wie man eine solche Gleichung löst, da es sich um eine Standardkonstruktion der Form $\left| handelt f\left(x \right) \right|=g\left(x \right)$. Aber versuchen wir, diese Gleichung aus einem etwas anderen Blickwinkel zu betrachten. Betrachten Sie genauer den Ausdruck unter dem Modulzeichen. Ich möchte Sie daran erinnern, dass der Modul einer beliebigen Zahl gleich der Zahl selbst sein oder dieser Zahl entgegengesetzt sein kann:

\[\left| a \right|=\left\( \begin(align)& a,\quad a\ge 0, \\& -a,\quad a \lt 0. \\\end(align) \right.\]

Tatsächlich ist diese Mehrdeutigkeit das ganze Problem: Da sich die Zahl unter dem Modul ändert (dies hängt von der Variablen ab), ist es für uns nicht klar, ob sie positiv oder negativ ist.

Was aber, wenn Sie zunächst verlangen, dass diese Zahl positiv ist? Zum Beispiel fordern wir, dass $3x-5 \gt 0$ – in diesem Fall erhalten wir garantiert eine positive Zahl unter dem Modulzeichen, und wir können genau dieses Modul vollständig loswerden:

Somit wird unsere Gleichung zu einer linearen Gleichung, die leicht gelöst werden kann:

Allerdings machen alle diese Gedanken nur unter der Bedingung $3x-5 \gt 0$ Sinn – wir haben diese Anforderung selbst eingeführt, um das Modul eindeutig zu offenbaren. Setzen wir daher das gefundene $x=\frac(5)(3)$ in diese Bedingung ein und prüfen:

Es stellt sich heraus, dass für den angegebenen Wert von $x$ unsere Anforderung nicht erfüllt ist, weil Es stellte sich heraus, dass der Ausdruck gleich Null war, und wir benötigen, dass er unbedingt größer als Null ist. Traurig. :(

Aber es ist okay! Schließlich gibt es noch eine andere Option: $3x-5 \lt 0$. Außerdem: Es gibt auch den Fall $3x-5=0$ – dieser muss ebenfalls berücksichtigt werden, sonst ist die Lösung unvollständig. Betrachten Sie also den Fall $3x-5 \lt 0$:

Offensichtlich wird das Modul mit einem Minuszeichen geöffnet. Doch dann entsteht eine seltsame Situation: Sowohl links als auch rechts in der ursprünglichen Gleichung wird derselbe Ausdruck hervorstechen:

Ich frage mich, bei welchem ​​$x$ der Ausdruck $5-3x$ gleich dem Ausdruck $5-3x$ sein wird? Sogar Captain Obviousness würde an solchen Gleichungen den Speichel verschlucken, aber wir wissen: Diese Gleichung ist eine Identität, d.h. es gilt für jeden Wert der Variablen!

Das bedeutet, dass jedes $x$ zu uns passt. Wir haben jedoch eine Einschränkung:

Mit anderen Worten: Die Antwort ist keine einzelne Zahl, sondern ein ganzes Intervall:

Schließlich bleibt noch ein weiterer Fall zu berücksichtigen: $3x-5=0$. Hier ist alles einfach: Unter dem Modul steht Null, und der Modul Null ist auch gleich Null (dies ergibt sich direkt aus der Definition):

Aber dann ist die ursprüngliche Gleichung $\left| 3x-5 \right|=5-3x$ wird wie folgt umgeschrieben:

Diese Wurzel haben wir oben bereits erhalten, als wir den Fall $3x-5 \gt 0$ betrachteten. Darüber hinaus ist diese Wurzel eine Lösung der Gleichung $3x-5=0$ – das ist die Einschränkung, die wir selbst eingeführt haben, um das Modul zurückzusetzen. :)

Somit geben wir uns neben dem Intervall auch mit der Zahl zufrieden, die ganz am Ende dieses Intervalls liegt:

Kombinieren von Wurzeln in Modulo-Gleichungen

Endgültige Gesamtantwort: $x\in \left(-\infty ;\frac(5)(3) \right]$ Es ist nicht sehr üblich, solchen Mist in der Antwort auf eine ziemlich einfache (im Wesentlichen lineare) Gleichung mit Modul zu sehen. Wirklich? Nun, gewöhnen Sie sich daran: Die Schwierigkeit des Moduls besteht darin, dass die Antworten in solchen Gleichungen völlig unvorhersehbar sein können.

Etwas anderes ist viel wichtiger: Wir haben gerade einen universellen Algorithmus zur Lösung einer Gleichung mit einem Modul analysiert! Und dieser Algorithmus besteht aus den folgenden Schritten:

1. Setzen Sie jeden Modul in der Gleichung mit Null gleich. Wir erhalten mehrere Gleichungen;
2. Lösen Sie alle diese Gleichungen und markieren Sie die Wurzeln auf der Zahlengeraden. Dadurch wird die Gerade in mehrere Intervalle unterteilt, in denen alle Module jeweils eindeutig aufgedeckt werden;
3. Lösen Sie die ursprüngliche Gleichung für jedes Intervall und kombinieren Sie Ihre Antworten.

Das ist alles! Es bleibt nur noch eine Frage: Was tun mit den in Schritt 1 erhaltenen Wurzeln? Nehmen wir an, wir haben zwei Wurzeln: $x=1$ und $x=5$. Sie werden den Zahlenstrahl in drei Teile teilen:

Den Zahlenstrahl mithilfe von Punkten in Intervalle aufteilen

Was sind also die Intervalle? Es ist klar, dass es drei davon gibt:

1. Ganz links: $x \lt 1$ – die Einheit selbst ist nicht im Intervall enthalten;
2. Zentral: $1\le x \lt 5$ – hier ist eins im Intervall enthalten, fünf jedoch nicht;
3. Ganz rechts: $x\ge 5$ - fünf ist nur hier enthalten!

Ich denke, Sie verstehen das Muster bereits. Jedes Intervall umfasst das linke Ende und nicht das rechte Ende.

Auf den ersten Blick mag ein solcher Eintrag unbequem, unlogisch und im Allgemeinen irgendwie verrückt erscheinen. Aber glauben Sie mir: Nach ein wenig Übung werden Sie feststellen, dass dieser Ansatz am zuverlässigsten ist und das eindeutige Öffnen der Module nicht beeinträchtigt. Es ist besser, ein solches Schema zu verwenden, als jedes Mal zu denken: Geben Sie dem aktuellen Intervall das linke/rechte Ende oder „werfen“ Sie es in das nächste.

MBOU-Sekundarschule Nr. 17, Ivanovo

« Gleichungen mit Modul
Methodische Entwicklung

Zusammengestellt

Mathelehrer

Lebedeva N.V.

20010

Erläuterungen

Kapitel 1 Einleitung

Abschnitt 2. Grundlegende Eigenschaften Abschnitt 3. Geometrische Interpretation des Konzepts des Moduls einer Zahl Abschnitt 4. Graph der Funktion y = |x| Abschnitt 5. Konventionen

Kapitel 2. Gleichungen lösen, die einen Modul enthalten

Abschnitt 1. Gleichungen der Form |F(x)| = m (am einfachsten) Abschnitt 2. Gleichungen der Form F(|x|) = m Abschnitt 3. Gleichungen der Form |F(x)| = G(x) Abschnitt 4. Gleichungen der Form |F(x)| = ± F(x) (am schönsten) Abschnitt 5. Gleichungen der Form |F(x)| = |G(x)| Abschnitt 6. Beispiele für die Lösung nicht standardmäßiger Gleichungen Abschnitt 7. Gleichungen der Form |F(x)| + |G(x)| = 0 Abschnitt 8. Gleichungen der Form |a 1 x ± b 1 | ± |a 2 x ± in 2 | ± …|a n x ± in n | = m Abschnitt 9. Gleichungen, die mehrere Module enthalten

Kapitel 3. Beispiele für die Lösung verschiedener Gleichungen mit Modul.

Abschnitt 1. Trigonometrische Gleichungen Abschnitt 2. Exponentialgleichungen Abschnitt 3. Logarithmische Gleichungen Abschnitt 4. Irrationale Gleichungen Abschnitt 5. Erweiterte Aufgaben Antworten zu den Übungen Referenzliste

Erläuterungen.

Der Begriff des Absolutwerts (Modul) einer reellen Zahl ist eines ihrer wesentlichen Merkmale. Dieses Konzept ist in verschiedenen Bereichen der physikalischen, mathematischen und technischen Wissenschaften weit verbreitet. In der Praxis des Mathematikunterrichts an weiterführenden Schulen gemäß dem Programm des Verteidigungsministeriums der Russischen Föderation wird der Begriff des „absoluten Wertes einer Zahl“ immer wieder angetroffen: In der 6. Klasse wird die Definition eines Moduls und seine geometrische Bedeutung wird vorgestellt; in der 8. Klasse wird der Begriff des absoluten Fehlers gebildet, die Lösung der einfachsten Gleichungen und Ungleichungen, die einen Modul enthalten, betrachtet und die Eigenschaften der arithmetischen Quadratwurzel untersucht; in der 11. Klasse findet sich das Konzept im Abschnitt „Wurzel N-ten Grades.“ Die Lehrerfahrung zeigt, dass Studierende bei der Lösung von Aufgaben, die Kenntnisse über diesen Stoff erfordern, häufig auf Schwierigkeiten stoßen und diese häufig überspringen, ohne mit der Bearbeitung begonnen zu haben. Ähnliche Aufgaben finden sich auch in den Texten der Prüfungsaufgaben für die Kurse der 9. und 11. Klasse. Darüber hinaus sind die Anforderungen, die Hochschulen an Schulabsolventen stellen, anders und zwar auf einem höheren Niveau als die Anforderungen des schulischen Lehrplans. Für das Leben in der modernen Gesellschaft ist die Ausbildung eines mathematischen Denkstils, der sich in bestimmten geistigen Fähigkeiten manifestiert, sehr wichtig. Bei der Lösung von Problemen mit Modulen ist die Fähigkeit erforderlich, Techniken wie Generalisierung und Spezifikation, Analyse, Klassifizierung und Systematisierung sowie Analogie anzuwenden. Durch die Lösung solcher Aufgaben können Sie Ihr Wissen über die Hauptabschnitte des Schulkurses, das Niveau des logischen Denkens und erste Recherchefähigkeiten testen. Diese Arbeit ist einem der Abschnitte gewidmet – dem Lösen von Gleichungen, die ein Modul enthalten. Es besteht aus drei Kapiteln. Im ersten Kapitel werden grundlegende Konzepte und die wichtigsten theoretischen Überlegungen vorgestellt. Das zweite Kapitel stellt neun Haupttypen von Gleichungen vor, die ein Modul enthalten, diskutiert Methoden zu deren Lösung und untersucht Beispiele unterschiedlicher Komplexität. Das dritte Kapitel bietet komplexere und nicht standardmäßige Gleichungen (trigonometrisch, exponentiell, logarithmisch und irrational). Für jeden Gleichungstyp gibt es Übungen zum eigenständigen Lösen (Lösungen und Anleitungen liegen bei). Der Hauptzweck dieser Arbeit besteht darin, Lehrkräften methodische Unterstützung bei der Unterrichtsvorbereitung und der Organisation von Wahlfächern zu bieten. Das Material kann auch als Lehrmittel für Oberstufenschüler verwendet werden. Die in der Arbeit vorgeschlagenen Aufgaben sind interessant und nicht immer leicht zu lösen, was es ermöglicht, die Bildungsmotivation der Schüler bewusster zu machen, ihre Fähigkeiten zu testen und den Grad der Vorbereitung der Schulabsolventen auf den Hochschulzugang zu erhöhen. Eine differenzierte Auswahl der vorgeschlagenen Übungen beinhaltet den Übergang von der reproduktiven Ebene der Beherrschung des Stoffes zur kreativen Ebene sowie die Möglichkeit, die Anwendung Ihres Wissens bei der Lösung nicht standardmäßiger Probleme zu lehren.

Kapitel 1 Einleitung.

Abschnitt 1. Bestimmung des Absolutwerts .

Definition : Der absolute Wert (Modul) einer reellen Zahl A eine nicht negative Zahl heißt: A oder -A. Bezeichnung: │ A │ Der Eintrag lautet wie folgt: „Modul der Zahl a“ oder „Absolutwert der Zahl a“

│ a, wenn a > 0

│a│ = │ 0, wenn a = 0 (1)

│ - und, wenn a
Beispiele: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Ausdrucksmodul erweitern:

a) │x - 8│, wenn x > 12 b) │2x + 3│, wenn x ≤ -2 │x – 8│= x – 8 │ 2x + 3│= - 2x – 3

Abschnitt 2. Grundlegende Eigenschaften.

Betrachten wir die grundlegenden Eigenschaften des absoluten Wertes. Eigenschaft Nr. 1: Gegenüberliegende Zahlen haben gleiche Module, d.h. │а│=│- à│ Zeigen wir, dass die Gleichheit wahr ist. Schreiben wir die Definition der Zahl auf - A : │- a│= (2) Vergleichen wir die Sätze (1) und (2). Offensichtlich sind die Definitionen der Absolutwerte von Zahlen A Und - A zusammenpassen. Somit, │а│=│- à│
Bei der Betrachtung der folgenden Eigenschaften beschränken wir uns auf deren Formulierung, da ihr Beweis in angegeben ist Eigenschaft Nr. 2: Der Absolutwert der Summe einer endlichen Anzahl reeller Zahlen überschreitet nicht die Summe der Absolutwerte der Terme: │а 1 + à 2 +…+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ Eigenschaft Nr. 3: Der Absolutwert der Differenz zwischen zwei reellen Zahlen überschreitet nicht die Summe ihrer Absolutwerte: │а - в│ ≤│а│+│в│ Eigenschaft Nr. 4: Der Absolutwert des Produkts einer endlichen Anzahl reeller Zahlen ist gleich dem Produkt der Absolutwerte der Faktoren: │а·в│=│а│·│в│ Eigenschaft Nr. 5: Der Absolutwert des Quotienten der reellen Zahlen ist gleich dem Quotienten ihrer Absolutwerte:

Abschnitt 3. Geometrische Interpretation des Konzepts des Moduls einer Zahl.

Jede reelle Zahl kann einem Punkt auf der Zahlenlinie zugeordnet werden, der ein geometrisches Abbild dieser reellen Zahl darstellt. Jeder Punkt auf der Zahlenlinie entspricht seinem Abstand vom Ursprung, d. h. die Länge des Segments vom Ursprung bis zu einem bestimmten Punkt. Dieser Abstand wird immer als nicht negativer Wert betrachtet. Daher ist die Länge des entsprechenden Segments die geometrische Interpretation des Absolutwerts einer bestimmten reellen Zahl

Die vorgestellte geometrische Darstellung bestätigt eindeutig Eigenschaft Nr. 1, d.h. die Moduli entgegengesetzter Zahlen sind gleich. Von hier aus ist die Gültigkeit der Gleichheit leicht zu verstehen: │х – а│= │а – x│. Auch die Lösung der Gleichung │х│= m mit m ≥ 0, nämlich x 1,2 = ± m, wird deutlicher. Beispiele: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
x 1,2 = 2; 4

Abschnitt 4. Graph der Funktion y = │х│

Der Definitionsbereich dieser Funktion sind alle reellen Zahlen.

Abschnitt 5. Konventionen.

In Zukunft werden bei der Betrachtung von Beispielen zur Lösung von Gleichungen die folgenden Konventionen verwendet: ( - Zeichen des Systems [ - Zeichen der Gesamtheit Beim Lösen eines Gleichungssystems (Ungleichungen) wird der Schnittpunkt der Lösungen der im System enthaltenen Gleichungen (Ungleichungen) ermittelt. Beim Lösen einer Menge von Gleichungen (Ungleichungen) wird die Vereinigung der in der Menge von Gleichungen (Ungleichungen) enthaltenen Lösungen gefunden.

Kapitel 2. Gleichungen lösen, die einen Modul enthalten.

In diesem Kapitel betrachten wir algebraische Methoden zum Lösen von Gleichungen, die ein oder mehrere Module enthalten.

Abschnitt 1. Gleichungen der Form │F (x)│= m

Eine Gleichung dieser Art nennt man die einfachste. Es gibt genau dann eine Lösung, wenn m ≥ 0. Nach Definition des Moduls entspricht die ursprüngliche Gleichung einem Satz von zwei Gleichungen: │ F(x)│=M
Beispiele:
№1. Lösen Sie die Gleichung: │7х - 2│= 9


Antwort: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Antwort: Die Summe der Wurzeln ist - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 bezeichnen wir x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5 m + 4 = 0 m = 1; 4 – beide Werte erfüllen die Bedingung m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Antwort: Anzahl der Wurzeln von Gleichung 7. Übungen:
№1. Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln an: │х - 5│= 3 №2 . Lösen Sie die Gleichung und geben Sie die kleinere Wurzel an: │x 2 + x│= 0 №3 . Lösen Sie die Gleichung und geben Sie die größere Wurzel an: │x 2 – 5x + 4│= 4 №4 .Lösen Sie die Gleichung und geben Sie die ganze Wurzel an: │2x 2 – 7x + 6│= 1 №5 .Lösen Sie die Gleichung und geben Sie die Anzahl der Wurzeln an: │x 4 – 13x 2 + 50│= 14

Abschnitt 2. Gleichungen der Form F(│х│) = m

Das Funktionsargument auf der linken Seite steht unter dem Modulzeichen und auf der rechten Seite ist es unabhängig von der Variablen. Betrachten wir zwei Möglichkeiten, Gleichungen dieser Art zu lösen. 1 Weg: Per Definition des Absolutwerts entspricht die ursprüngliche Gleichung der Kombination zweier Systeme. In jedem Fall wird einem submodularen Ausdruck eine Bedingung auferlegt. F(│x│) =M
Da die Funktion F(│x│) im gesamten Definitionsbereich gerade ist, sind die Wurzeln der Gleichungen F(x) = m und F(- x) = m Paare entgegengesetzter Zahlen. Daher reicht es aus, eines der Systeme zu lösen (bei der Betrachtung von Beispielen auf diese Weise wird die Lösung für ein System angegeben). Methode 2: Anwendung der Methode zur Einführung einer neuen Variablen. In diesem Fall wird die Bezeichnung │x│= a eingeführt, wobei a ≥ 0. Diese Methode ist weniger umfangreich im Design.
Beispiele: №1 . Lösen Sie die Gleichung: 3x 2 – 4│x│= - 1 Lassen Sie uns die Einführung einer neuen Variablen verwenden. Bezeichnen wir │x│= a, wobei a ≥ 0. Wir erhalten die Gleichung 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Zurück zur ursprünglichen Variablen: │ x│=1 und │х│= 1/3. Jede Gleichung hat zwei Wurzeln. Antwort: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Lösen Sie die Gleichung: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2
Finden wir die Lösung für das erste System der Grundgesamtheit: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Beachten Sie, dass x 2 nicht erfüllt die Bedingung x ≥ 0. Lösung Das zweite System wird die Zahl sein, die dem Wert x 1 entgegengesetzt ist. Antwort: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Lösen Sie die Gleichung: x 4 – │х│= 0 Bezeichnen wir │х│= a, wobei a ≥ 0. Wir erhalten die Gleichung a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Rückkehr zur ursprünglichen Variablen: │х│=0 und │х│= 1 x = 0; ± 1 Antwort: x 1 = 0; X 2 = 1; X 3 = - 1.
Übungen: №6. Lösen Sie die Gleichung: 2│х│ - 4,5 = 5 – 3 / 8 │х│ №7 . Lösen Sie die Gleichung und geben Sie die Anzahl der Wurzeln in Ihrer Antwort an: 3x 2 - 7│x│ + 2 = 0 №8 . Lösen Sie die Gleichung und geben Sie in Ihrer Antwort ganzzahlige Lösungen an: x 4 + │x│ - 2 = 0

Abschnitt 3. Gleichungen der Form │F(x)│ = G(x)

Die rechte Seite einer solchen Gleichung hängt von einer Variablen ab und hat daher genau dann eine Lösung, wenn die rechte Seite eine Funktion G(x) ≥ 0 ist. Die ursprüngliche Gleichung kann auf zwei Arten gelöst werden : 1 Weg: Standard, der auf der Offenlegung eines Moduls basierend auf seiner Definition basiert und aus einem gleichwertigen Übergang zu einer Kombination zweier Systeme besteht. │ F(x)│ =G(X)

Diese Methode kann bei einem komplexen Ausdruck für die Funktion G(x) und einem weniger komplexen Ausdruck für die Funktion F(x) sinnvoll angewendet werden, da davon ausgegangen wird, dass Ungleichungen mit der Funktion F(x) gelöst werden. Methode 2: Besteht im Übergang zu einem äquivalenten System, in dem auf der rechten Seite eine Bedingung gestellt wird. │ F(X)│= G(X)

Diese Methode ist bequemer anzuwenden, wenn der Ausdruck für die Funktion G(x) weniger komplex ist als für die Funktion F(x), da die Lösung der Ungleichung G(x) ≥ 0 angenommen wird. Darüber hinaus im Fall Bei mehreren Modulen empfiehlt es sich, die zweite Möglichkeit zu nutzen. Beispiele: №1. Lösen Sie die Gleichung: │x + 2│= 6 -2x
(1 Weg) Antwort: x = 1 1 / 3 №2.
│х 2 – 2х - 1│= 2·(x + 1)
(2-Wege) Antwort: Das Produkt der Wurzeln ist 3.
№3. Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln in Ihrer Antwort an:
│x - 6│= x 2 - 5x + 9

Antwort: Die Summe der Wurzeln ist 4.
Übungen: №9. │x + 4│= - 3x №10. Lösen Sie die Gleichung und geben Sie die Anzahl der Lösungen in Ihrer Antwort an:│x 2 + x - 1│= 2x – 1 №11 . Lösen Sie die Gleichung und geben Sie das Produkt der Wurzeln in Ihrer Antwort an:│x + 3│= x 2 + x – 6

Abschnitt 4. Gleichungen der Form │F(x)│= F(x) und │F(x)│= - F(x)

Gleichungen dieser Art werden manchmal als „die schönsten“ bezeichnet. Da die rechte Seite der Gleichungen von der Variablen abhängt, gibt es genau dann Lösungen, wenn die rechte Seite nicht negativ ist. Daher sind die ursprünglichen Gleichungen äquivalent zu den Ungleichungen:
│F(x)│= F(x) F(x) ≥ 0 und │F(x)│= - F(x) F(x) Beispiele: №1 . Lösen Sie die Gleichung und geben Sie die kleinere ganzzahlige Wurzel in Ihrer Antwort an: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Antwort: x = 1№2. Lösen Sie die Gleichung und geben Sie die Länge des Intervalls in Ihrer Antwort an: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Antwort: Die Länge des Intervalls beträgt 6.№3 . Lösen Sie die Gleichung und geben Sie die Anzahl der ganzzahligen Lösungen in Ihrer Antwort an: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Antwort: 4 ganze Lösungen.№4 . Lösen Sie die Gleichung und geben Sie die größte Wurzel in Ihrer Antwort an:
│4 – x -
│= 4 – x –
x 2 – 5x + 5 = 0 D = 5 x 1,2 =
≈ 1,4

Antwort: x = 3.

Übungen: №12. Lösen Sie die Gleichung und geben Sie in Ihrer Antwort die ganze Wurzel an: │x 2 + 6x + 8│= x 2 + 6x + 8 №13. Lösen Sie die Gleichung und geben Sie die Anzahl der ganzzahligen Lösungen in Ihrer Antwort an: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Lösen Sie die Gleichung. Geben Sie in Ihrer Antwort eine ganze Zahl an, die nicht die Wurzel der Gleichung ist:

Abschnitt 5. Gleichungen der Form │F(x)│= │G(x)│

Da beide Seiten der Gleichung nicht negativ sind, umfasst die Lösung die Betrachtung zweier Fälle: Submodulare Ausdrücke haben das gleiche oder entgegengesetzte Vorzeichen. Daher entspricht die ursprüngliche Gleichung der Kombination zweier Gleichungen: │ F(X)│= │ G(X)│
Beispiele: №1. Lösen Sie die Gleichung und geben Sie in Ihrer Antwort die ganze Wurzel an: │x + 3│=│2x - 1│
Antwort: ganze Wurzel x = 4.№2. Löse die Gleichung: │ x – x 2 - 1│=│2x – 3 – x 2 │
Antwort: x = 2.№3 . Lösen Sie die Gleichung und geben Sie das Produkt der Wurzeln in Ihrer Antwort an:




Wurzelgleichungen 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Antwort: Das Produkt der Wurzeln ist – 0,25. Übungen: №15 . Lösen Sie die Gleichung und geben Sie in Ihrer Antwort die gesamte Lösung an: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16. Lösen Sie die Gleichung und geben Sie die kleinere Wurzel in Ihrer Antwort an:│5x - 3│=│7 - x│ №17 . Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln in Ihrer Antwort an:

Abschnitt 6. Beispiele für die Lösung nicht standardmäßiger Gleichungen

In diesem Abschnitt betrachten wir Beispiele für nicht standardmäßige Gleichungen, bei deren Lösung der Absolutwert des Ausdrucks per Definition ermittelt wird. Beispiele:

№1. Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln in Ihrer Antwort an: x · │x│- 5x – 6 = 0
Antwort: Die Summe der Wurzeln ist 1 №2. . Lösen Sie die Gleichung und geben Sie die kleinere Wurzel in Ihrer Antwort an: x 2 - 4x ·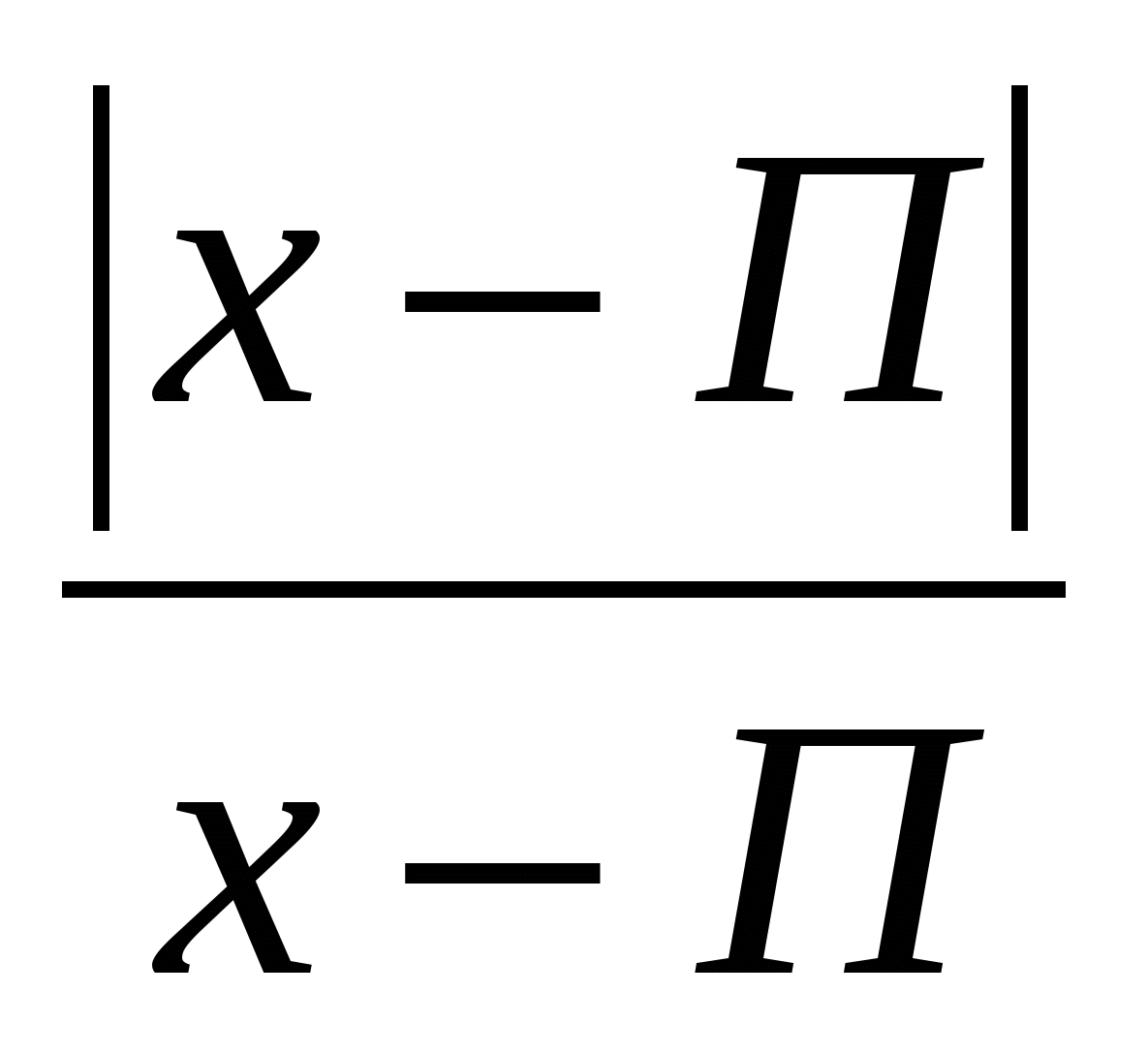
- 5 = 0
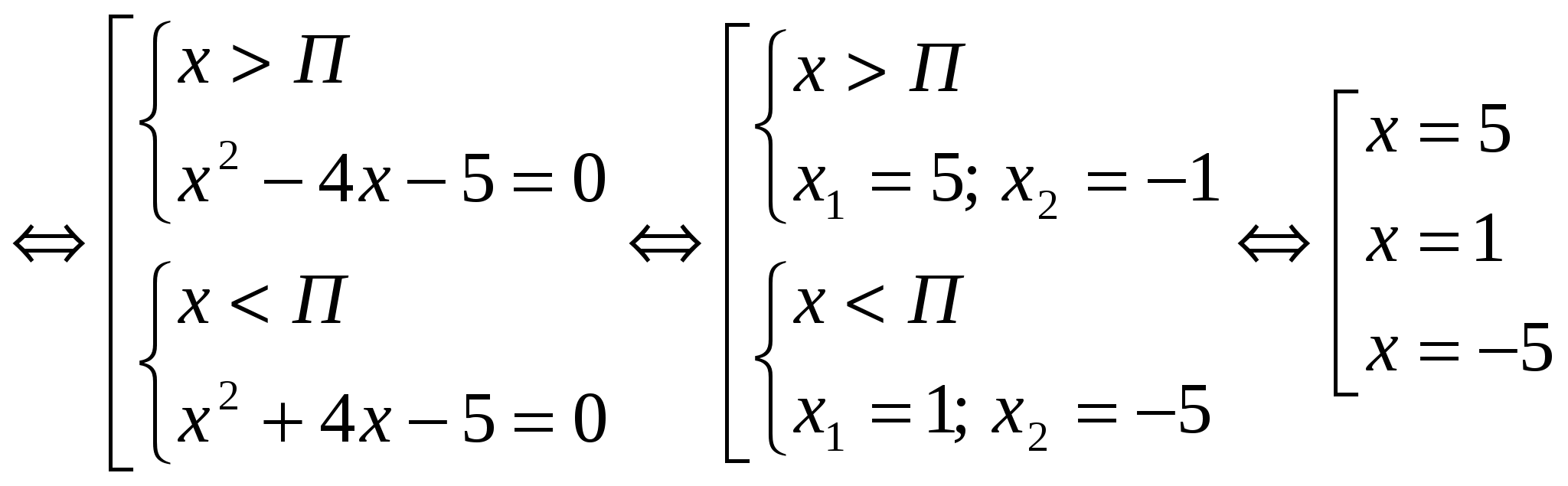Antwort: kleinere Wurzel x = - 5. №3. Löse die Gleichung:

Antwort: x = -1. Übungen: №18. Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln an: x · │3x + 5│= 3x 2 + 4x + 3
№19. Lösen Sie die Gleichung: x 2 – 3x =

№20. Löse die Gleichung:

Abschnitt 7. Gleichungen der Form │F(x)│+│G(x)│=0

Es ist leicht zu erkennen, dass auf der linken Seite einer Gleichung dieses Typs die Summe nichtnegativer Größen steht. Daher hat die ursprüngliche Gleichung genau dann eine Lösung, wenn beide Terme gleichzeitig gleich Null sind. Die Gleichung entspricht dem Gleichungssystem: │ F(X)│+│ G(X)│=0
Beispiele: №1 . Löse die Gleichung:
Antwort: x = 2. №2. Löse die Gleichung: Antwort: x = 1. Übungen: №21. Löse die Gleichung: №22 . Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln in Ihrer Antwort an: №23 . Lösen Sie die Gleichung und geben Sie die Anzahl der Lösungen in Ihrer Antwort an:

Abschnitt 8. Gleichungen der Form │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m

Um Gleichungen dieser Art zu lösen, wird die Intervallmethode verwendet. Wenn wir es durch sequentielle Erweiterung von Modulen lösen, erhalten wir N von Systemen, was sehr umständlich und unpraktisch ist. Betrachten wir den Algorithmus der Intervallmethode: 1). Finden Sie Variablenwerte X, für die jedes Modul gleich Null ist (Nullen submodularer Ausdrücke):
2). Markieren Sie die gefundenen Werte auf einem Zahlenstrahl, der in Intervalle unterteilt ist (die Anzahl der Intervalle ist jeweils gleich). N+1 ) 3). Bestimmen Sie, mit welchem ​​Vorzeichen jedes Modul in jedem der erhaltenen Intervalle angezeigt wird (bei der Lösungsfindung können Sie einen Zahlenstrahl verwenden und die Vorzeichen darauf markieren) 4). Die ursprüngliche Gleichung entspricht dem Aggregat N+1 Systeme, in denen jeweils die Zugehörigkeit der Variablen angegeben ist X eines der Intervalle. Beispiele: №1 . Lösen Sie die Gleichung und geben Sie die größte Wurzel in Ihrer Antwort an:
1). Finden wir die Nullstellen der submodularen Ausdrücke: x = 2; x = -3 2). Markieren wir die gefundenen Werte auf dem Zahlenstrahl und bestimmen wir, mit welchem ​​Vorzeichen jedes Modul in den resultierenden Intervallen aufgedeckt wird:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- keine Lösungen Die Gleichung hat zwei Wurzeln. Antwort: Die größte Wurzel x = 2. №2. Lösen Sie die Gleichung und geben Sie in Ihrer Antwort die ganze Wurzel an:
1). Finden wir die Nullstellen der submodularen Ausdrücke: x = 1,5; x = - 1 2). Markieren wir die gefundenen Werte auf dem Zahlenstrahl und bestimmen wir, mit welchem ​​Vorzeichen jedes Modul in den resultierenden Intervallen aufgedeckt wird: x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).
Das letzte System hat keine Lösungen, daher hat die Gleichung zwei Wurzeln. Beim Lösen der Gleichung sollten Sie auf das „-“-Zeichen vor dem zweiten Modul achten. Antwort: ganze Wurzel x = 7. №3. Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln in Ihrer Antwort an: 1). Finden wir die Nullstellen der submodularen Ausdrücke: x = 5; x = 1; x = - 2 2). Markieren wir die gefundenen Werte auf dem Zahlenstrahl und bestimmen wir, mit welchem ​​Vorzeichen jedes Modul in den resultierenden Intervallen aufgedeckt wird: x – 5 x – 5 x – 5 x – 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Die Gleichung hat zwei Wurzeln x = 0 und 2. Antwort: Die Summe der Wurzeln ist 2. №4 . Lösen Sie die Gleichung: 1). Finden wir die Nullstellen der submodularen Ausdrücke: x = 1; x = 2; x = 3. 2). Lassen Sie uns bestimmen, mit welchem ​​Vorzeichen jedes Modul in den resultierenden Intervallen angezeigt wird. 3).
Kombinieren wir die Lösungen der ersten drei Systeme. Antwort: ; x = 5.
Übungen: №24. Löse die Gleichung:
№25. Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln in Ihrer Antwort an: №26. Lösen Sie die Gleichung und geben Sie in Ihrer Antwort die kleinere Wurzel an: №27. Lösen Sie die Gleichung und geben Sie in Ihrer Antwort die größere Wurzel an:

Abschnitt 9. Gleichungen, die mehrere Module enthalten

Gleichungen, die mehrere Module enthalten, gehen davon aus, dass in submodularen Ausdrücken absolute Werte vorhanden sind. Das Grundprinzip zur Lösung derartiger Gleichungen ist die sequentielle Offenlegung von Modulen, beginnend mit dem „externen“. Bei der Lösung kommen die in den Abschnitten Nr. 1, Nr. 3 besprochenen Techniken zum Einsatz.

Beispiele: №1. Löse die Gleichung:
Antwort: x = 1; - elf. №2. Löse die Gleichung:
Antwort: x = 0; 4; - 4. №3. Lösen Sie die Gleichung und geben Sie das Produkt der Wurzeln in Ihrer Antwort an:
Antwort: Das Produkt der Wurzeln ist – 8. №4. Löse die Gleichung: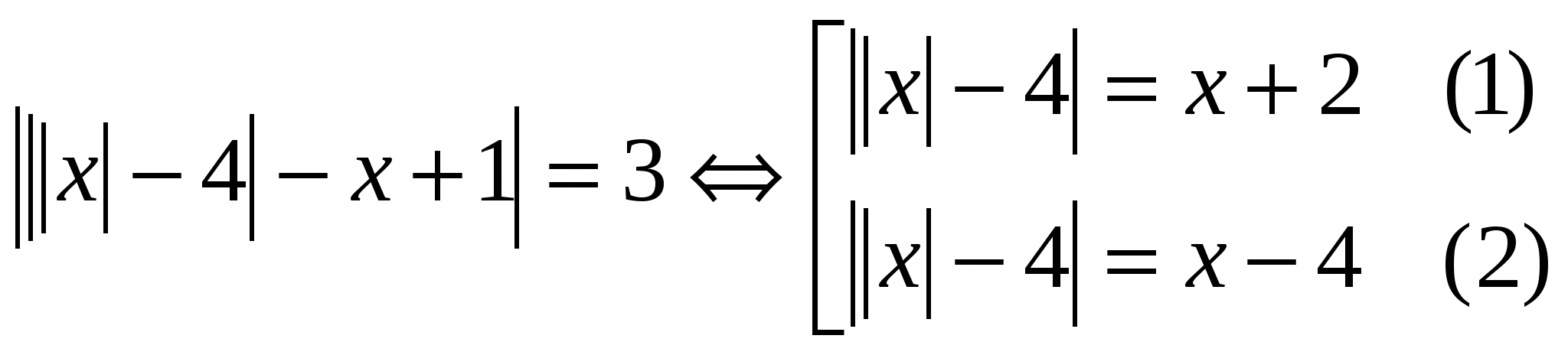
Bezeichnen wir die Gleichungen der Bevölkerung (1) Und (2) und überlegen Sie sich die Lösung für jedes davon separat, um das Design zu vereinfachen. Da beide Gleichungen mehr als ein Modul enthalten, ist es bequemer, einen äquivalenten Übergang zu Systemmengen durchzuführen. (1)

(2)


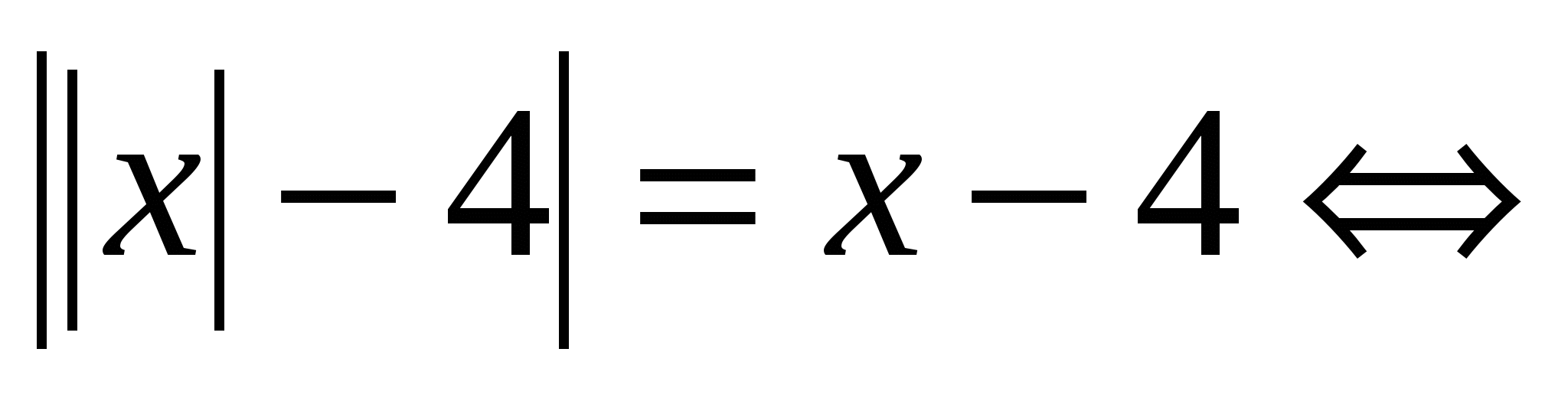
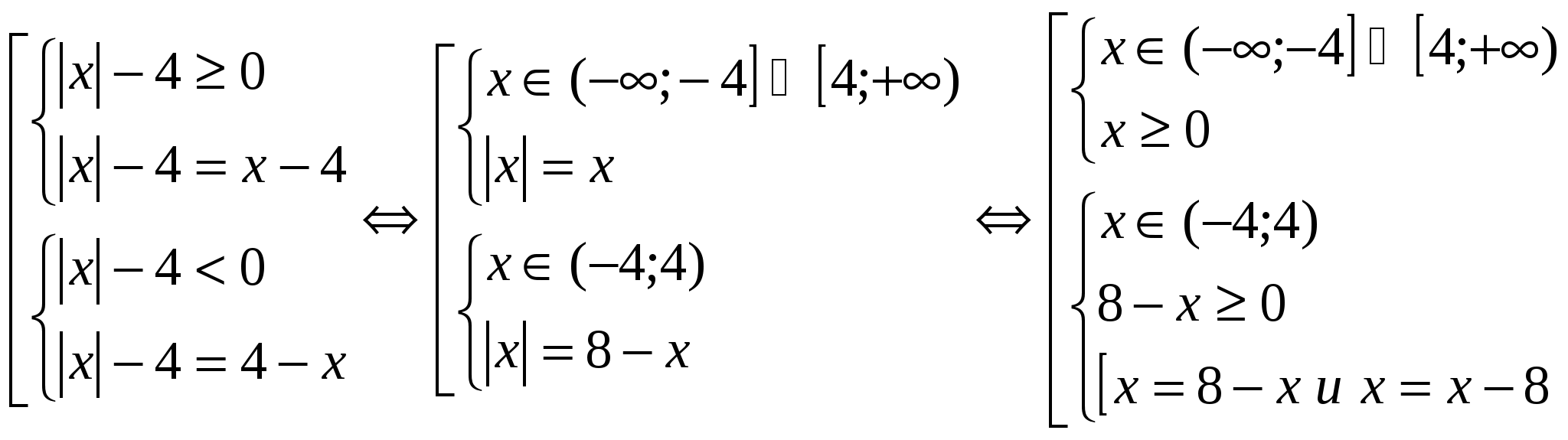
Antwort:
Übungen: №36. Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln in Ihrer Antwort an: 5 │3x-5│ = 25 x №37. Lösen Sie die Gleichung. Wenn es mehr als eine Wurzel gibt, geben Sie die Summe der Wurzeln in Ihrer Antwort an: │x + 2│ x – 3x – 10 = 1 №38. Lösen Sie die Gleichung: 3 │2x -4│ = 9 │x│ №39. Lösen Sie die Gleichung und geben Sie die Anzahl der Wurzeln in Ihrer Antwort an: 2 │ sin x│ = √2 №40 . Lösen Sie die Gleichung und geben Sie die Anzahl der Wurzeln in Ihrer Antwort an:

Abschnitt 3. Logarithmische Gleichungen.

Bevor Sie die folgenden Gleichungen lösen, müssen Sie die Eigenschaften von Logarithmen und der logarithmischen Funktion überprüfen. Beispiele: №1. Lösen Sie die Gleichung und geben Sie das Produkt der Wurzeln in Ihrer Antwort an: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1

Fall 1: Wenn x ≥ - 1, dann log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – erfüllt die Bedingung x ≥ - 1 2 Fall: wenn x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – erfüllt die Bedingung x - 1
Antwort: Das Produkt der Wurzeln ist – 15.
№2. Lösen Sie die Gleichung und geben Sie die Summe der Wurzeln in Ihrer Antwort an: lg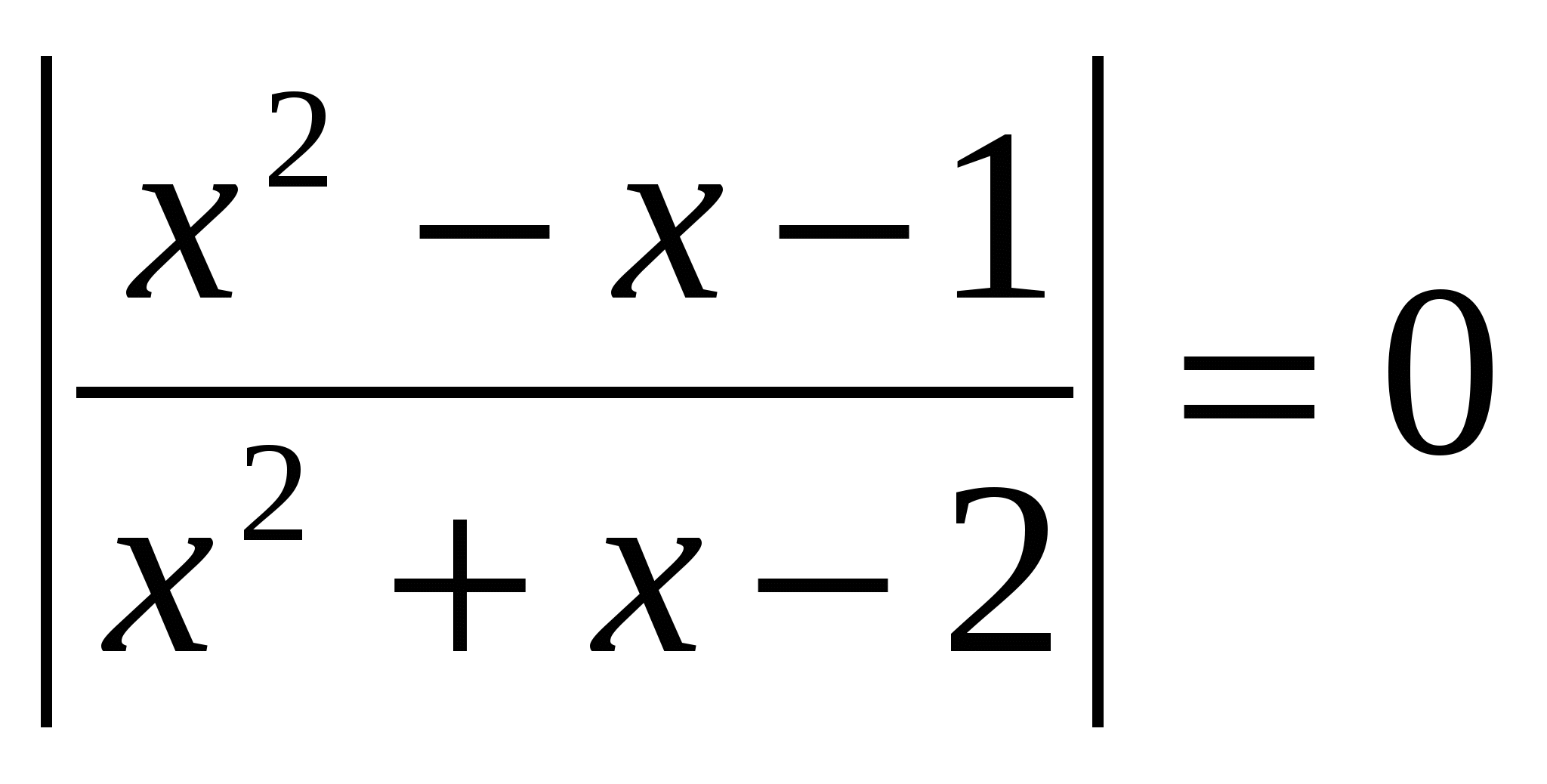
O.D.Z.

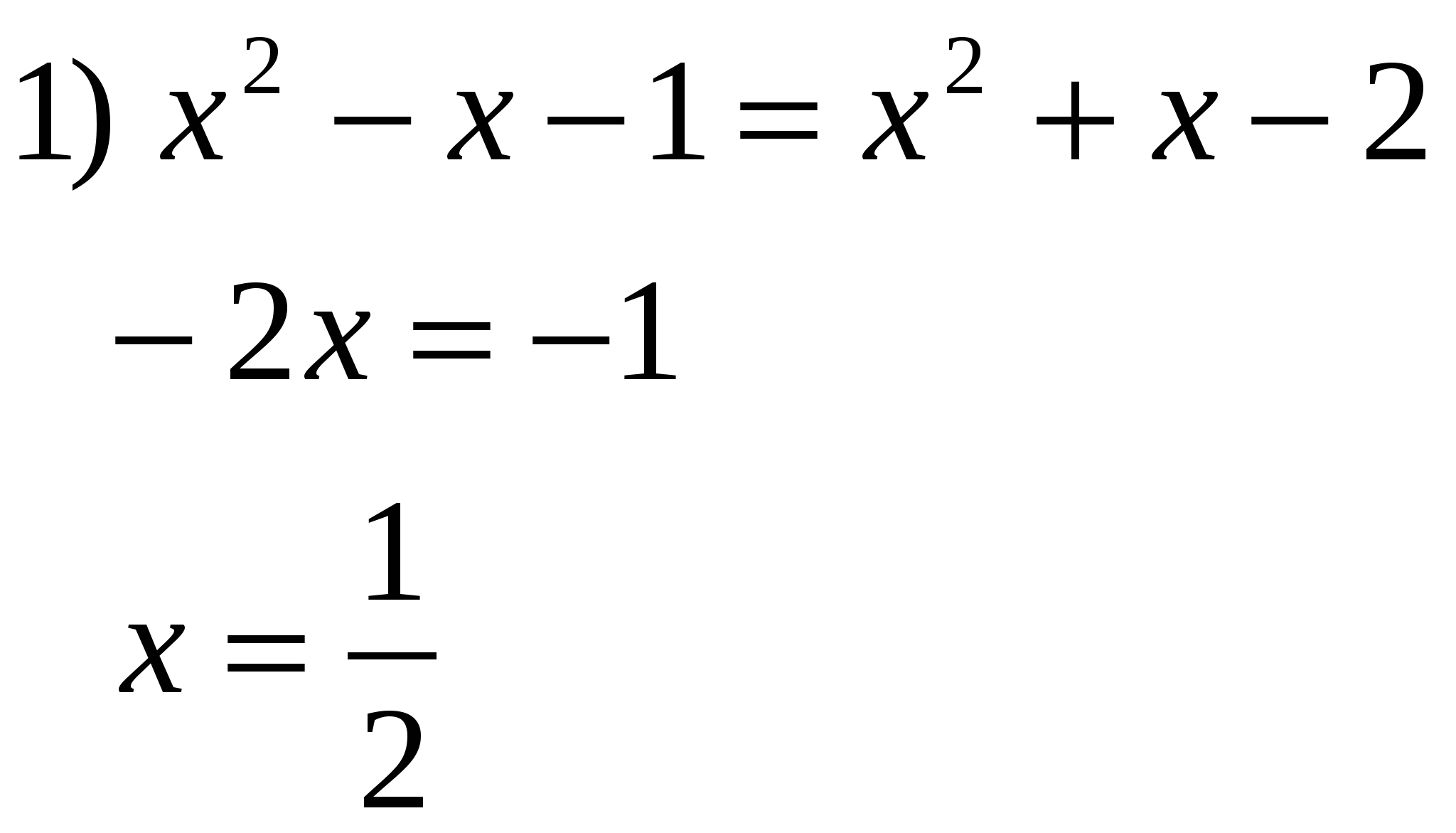
Antwort: Die Summe der Wurzeln beträgt 0,5.
№3. Lösen Sie die Gleichung: log 5
O.D.Z.

Antwort: x = 9. №4. Lösen Sie die Gleichung: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Verwenden wir die Formel für den Übergang zu einer anderen Basis. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Finden wir die Nullstellen der submodularen Ausdrücke: x = 25; x = Diese Zahlen unterteilen den Bereich akzeptabler Werte in drei Intervalle, sodass die Gleichung einer Menge von drei Systemen entspricht.
Antwort: )